Unidad 3 Redes by on Scribd
Aplicacion de matematicas discretas
viernes, 21 de junio de 2019
viernes, 14 de junio de 2019
Problema del Agente Viajero
Problema del Agente Viajero
Este tipo de problemas tiene gran aplicación en el ámbito de la logística y distribución, así como en la programación de curvas de producción.
El problema del agente viajero tiene una variación importante, y esta depende de que las distancias entre un nodo y otro sean simétricas o no, es decir, que la distancia entre A y B sea igual a la distancia entre B y A, puesto que en la práctica es muy poco probable que así sea.
La cantidad de rutas posibles en una red está determinada por la ecuación:
(n-1)!
Es decir que en una red de 5 nodos la cantidad de rutas probables es igual a (5-1)! = 24, y a medida que el número de nodos aumente la cantidad de rutas posibles crece factorialmente. En el caso de que el problema sea simétrico la cantidad de rutas posibles se reduce a la mitad, es decir:
( (n-1)! ) / 2
Lo cual significa un ahorro significativo en el tiempo de procesamiento de rutas de gran tamaño.
MÉTODOS DE SOLUCIÓN
La complejidad del cálculo del problema del agente viajero ha despertado múltiples iniciativas por mejorar la eficiencia en el cálculo de rutas. El método más básico es el conocido con el nombre de fuerza bruta, que consiste en el cálculo de todos los posibles recorridos, lo cual se hace extremadamente ineficiente y casi que se imposibilita en redes de gran tamaño. También existen heurísticos que se han desarrollado por la complejidad en el cálculo de soluciones óptimas en redes robustas, es por ello que existen métodos como el vecino más cercano, la inserción más barata y el doble sentido. Por último se encuentran los algoritmos que proporcionan soluciones óptimas, como el método de branch and bound (ramificación y poda), que trabaja el problema como un algoritmo de asignación y lo resuelve por medio del método simplex.
Posibles rutas
A - B - D - C - A = 9 + 15 + 4 + 7 = 35 km
A - B - C - D - A = 9 + 10 + 4 + 8 = 31 km
A - C - B - D - A = 7 + 10 + 15 + 8 = 40 km
Rutas simétricas
A - D - C - B - A = 8 + 4 + 10 + 9 = 31 km
A - C - D - B - A = 7 + 4 + 15 + 9 = 35 km
A - D - B - C - A = 8 + 15 + 10 +7 = 40 km
MÉTODO DEL VECINO MÁS CERCANO
El método del vecino más cercano es un algoritmo eucarístico diseñado para solucionar el problema del agente viajero, no asegura una solución óptima, sin embargo suele proporcionar buenas soluciones, y tiene un tiempo de cálculo muy eficiente. El método de desarrollo es muy similar al utilizado para resolver problemas de árbol de expansión mínima.

El método consiste en una vez establecido el nodo de partida, evaluar y seleccionar su vecino más cercano. En este caso:

En la siguiente iteración habrá que considerar los vecinos más cercanos al nodo C (se excluye A por ser el nodo de origen):

En la siguiente iteración los vecinos más cercanos de D serán C, con quien ya tiene conexión, A quién es el nodo de origen y B, por esta razón B se debe seleccionar por descarte. Al estar en B todos los nodos se encuentran visitados, por lo que corresponde a cerrar la red uniendo el nodo B con el nodo A, así entonces la ruta solución por medio del vecino más próximo sería A, C, D, B, A = 7, 4, 15, 9 = 35 km.
Este es un caso en el que a pesar de tener una red compuesta por pocos nodos, el método del vecino más cercano no proporciona la solución óptima, la cual calculamos con el método de fuerza bruta como 31 km.
Cuestionario
1°-¿Cual es el objetivo del Problema del gente Viajero?
El objetivo es encontrar un recorrido completo que conecte todos los nodos de una red, visitándolos tan solo una vez y volviendo al punto de partida.
2°-¿Este tipo de problemas en que ámbito se aplica?
Este tipo de problemas tiene gran aplicación en el ámbito de la logística y distribución, así como en la programación de curvas de producción.
3°-Menciona los métodos que conoces para solucionar el problema.
-Método de Fuerza Bruta
-Método del vecino mas cercano
-Método de Branch and Bound
4°-¿En que consiste el método de Fuerza Bruta?
El método de la fuerza bruta no implica la aplicación de ningún algoritmo sistemático, tan solo consiste en explorar todos los recorridos posibles.
5°-¿En que consiste el método del vecino mas cercano?
El método de desarrollo es muy similar al utilizado para resolver problemas de árbol de expansión mínima.
6°-¿Qué es el método del vecino mas cercano?
El método del vecino más cercano es un algoritmo heurístico diseñado para solucionar el problema del agente viajero, no asegura una solución óptima, sin embargo suele proporcionar buenas soluciones, y tiene un tiempo de cálculo muy eficiente.
7°-¿En que consiste el método del vecino mas cercano?
El método consiste en una vez establecido el nodo de partida, evaluar y seleccionar su vecino más cercano.
8°-Describe el Agente Viajero.
En el problema se presentan N! rutas posibles, aunque se puede simplificar ya que dada una ruta nos da igual el punto de partida.
9°-¿Que nos proporciona el método de Branch and Bound?
El método de branch and bound(ramificación y poda), nos proporciona una solución óptima del problema del agente viajero, calculando mediante el algoritmo simplex la solución del modelo.
10°-¿Como es el origen del Agente Viajero?
El origen de los problemas del agente viajero no esta claro.Una guía para agentes viajeros de 1832 menciona el problema e incluye ejemplos de viajes a traves de Alemania y Suiza.
jueves, 30 de mayo de 2019
¿Qué es un Mapa de Karnaugh?
Los Mapas de Karnaugh son una herramienta muy utilizada para la simplificación de circuitos lógicos. Cuando se tiene una función lógica con su tabla de verdad y se desea implementar esa función de la manera más económica posible se utiliza este método.
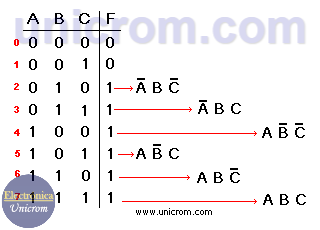
Ejemplo: Se tiene la siguiente tabla de verdad para tres variables. Se desarrolla la función lógica basada en ella. (primera forma canónica). Ver que en la fórmula se incluyen solamente las variables (A, B, C) cuando F cuando es igual a “1”. Si A en la tabla de verdad es “0” se pone A, si B = “1” se pone B, Si C = “0” se pone C, etc.
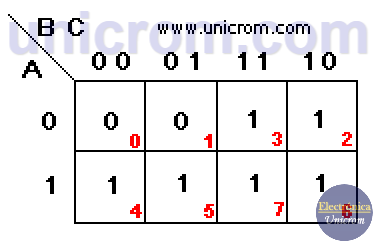
Una vez obtenida la función lógica, se implementa el mapa de Karnaugh. Este tiene 8 casillas que corresponden a 2n, donde n = 3 (número de variables (A, B, C)). Ver el diagrama arriba. La primera fila corresponde a A = 0 La segunda fila corresponde a A = 1 La primera columna corresponde a BC = 00 (B=0 y C=0).
La segunda columna corresponde a BC = 01 (B=0 y C=1) La tercera columna corresponde a BC = 11 (B=1 y C=1) La cuarta columna corresponde a BC = 10 (B=1 y C=0)
En el mapa de Karnaugh se han puesto “1” en las casillas que corresponden a los valores de F = “1” en la tabla de verdad. Tomar en cuenta la numeración de las filas de la tabla de verdad y la numeración de las casillas en el mapa de Karnaugh.
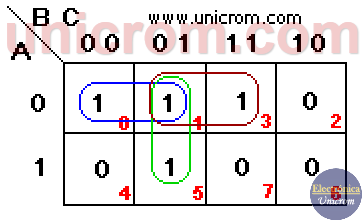
Para proceder con la simplificación, se crean grupos de “1”s que tengan 1, 2, 4, 8, 16, etc. (sólo potencias de 2). Los “1”s deben estar adyacentes (no en diagonal) y mientras más “1”s tenga el grupo, mejor. La función mejor simplificada es aquella que tiene el menor número de grupos con el mayor número de “1”s en cada grupo
Se ve del gráfico que hay dos grupos cada uno de cuatro “1”s, (se permite compartir casillas entre los grupos). La nueva expresión de la función boolena simplificada se deduce del mapa de Karnaugh.
- Para el primer grupo (rojo): la simplificación da B (los “1”s de la tercera y cuarta columna corresponden a B sin negar)
- Para el segundo grupo (azul): la simplificación da A (los “1”s están en la fila inferior que corresponde a A sin negar).
Entonces el resultado es F = B + A ó F = A + B
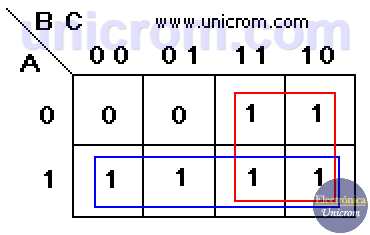
Ejemplo: Una tabla de verdad como la de la derecha da la siguiente función booleana: F = A B C + A B C + A B C + A B C
Se ve claramente que la función es un reflejo del contenido de la tabla de verdad cuando F = “1”, Con esta ecuación se crea el mapa de Karnaugh y se escogen los grupos. Se lograron hacer 3 grupos de dos “1”s cada uno. Se puede ver que no es posible hacer grupos de 3, porque 3 no es potencia de 2. Se observa que hay una casilla que es compartida por los tres grupos.
La función simplificada es: F = A B+ A C + B C. Grupo en azul: A B, grupo marrón: A C, grupo verde:B C
CUESTIONARIO
1°-¿Que es un mapa de Karnaugh?
Los Mapas de Karnaugh son una herramienta muy utilizada para la simplificación de circuitos lógicos.
2°-¿Cuando se invento el Mapa de karnaugh?
El mapa de Karnaugh fue inventado en 1953 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.
3°-¿En que consiste el Mapa de Karnaugh?
El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar.
4°-¿Como se ordenan las variables de la expresión?
Las variables de la expresión son ordenadas en función de su peso y siguiendo el código Gray, de manera que sólo una de las variables varía entre celdas adyacentes.
5°-¿Cuando se utiliza un Mapa de Karnaugh?
Los diagramas de Karnaugh pueden ser utilizados en la simplificación de sentencias definidas en lógica Booleana, construcción de estaciones de clasificación, selección y control de calidad de piezas fabricadas, entre otras aplicaciones.
6°-¿Como se representa el numero de renglones y columnas de un Mapa de Karnaugh?
El número de renglones y columnas de un mapa de Karnaugh normalmente suele representarse como un mapa cuadrado (número de renglones = número de columnas) cuando el número de variables es par (2, 4, 6, 8... etc) y cuando el número de variables es impar el número de renglones igual a la mitad del número de columnas.
7°-Menciona un software disponible para asistir el mapeo de Karnaugh
- Gorgeus Karnaugh K-Mapas minimización programa
8°-¿Cuales son las ventajas de usar el Mapa de Karnaugh?
Los mapas de Karnaugh reducen la necesidad de hacer cálculos extensos para la simplificación de expresiones booleanas.
9°-¿Cómo se realizan las tablas de Karnaugh?
Las tablas de Karnaugh se pueden fácilmente realizar a mano con funciones de hasta 6 variables, para funciones de mayor cantidad de variables es más eficiente el uso de software especializado.
10°-¿Con que otro nombre se conoce a los Mapas de Karnaugh?
También conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como Mapa-K o Mapa-KV.
domingo, 14 de abril de 2019
TÉCNICAS DE CONTEO
- Diagrama de árbol
- Permutaciones
- Entran todos los elementos.
- Si importa el orden.
- No se repitan los elementos.
Si el ejercicio que se plantea sigue estas tres reglas la formula es aplicar Pn=n!
- Variaciones
- Combinaciones
Ejercicios Permutaciones
- ¿Cuantos números de 3 cifras diferentes se puede formar con los dígitos 1,2,3?
3*2*1=6 1,2,3
1,3,2
2,3,1
2,1,3
3,1,2
3,2,1
2.¿Cuantos grupos diferentes de tres vocales se puede formar sin que se repitan los elementos, usando 3 vocales: A,E,O?
3*2*1=6 A,E,O
A,O,E
E,A,O
E,O,A
O,A,E
O,E,A
3.¿Cuantos grupos de 4 elementos se puede formar con los digitos 3,5,7,9?
P4=4! 4*3*2*1=24
3,5,7,9 5,3,7,9 7,5,9,3 9,3,5,7
3,5,9,7 5,3,9,7 7,5,3,9 9,3,7,5
3,9,7,5 5,9,3,7 7,3,5,9 9,7,3,5
3,9,5,7 5,9,7,3 7,3,9,5 9,7,5,3
3,7,9,5 5,7,3,9 7,9,3,5 9,5,3,7
3,7,5,9 5,7,9,3 7,9,5,3 9,5,7,3
4. Antiguamente los barcos se comunicaban entre si usando banderas de diferentes colores de manera ordenada.
P4=4!
4*3*2*1= 24 mensajes
P5=5!
5*4*3*2*1=120 mensajes
Permutaciones con repetición
Se llama permutaciones con repetición a los grupos de elementos que se forman cuando "n" elementos,donde e primer elemento se repite n veces, el segundo también se repite n veces y así se repiten hasta llegar al final de la lista. Estas agrupaciones deben seguir las siguientes reglas;
- Entran todos los elementos.
- Si importa el orden.
- Si se repiten los elementos.
La formula para realizar el calculo de las permutaciones con repetición es la siguiente.
PRn=____Pn_____
a! b! c!
Con las cifras 2,2,2,3,3,3,3,4,4 ¿Cuantos números de 9 cifras se pueden formar? Si los datos son n=9 a=3 b=4 c=2
abc
PRn =____Pn______
a! b! c!
3,4,2
PRn =______Pa______= 9*8*7*6*5*4*3*2*1= 9*8*7*6 = 15120 = 1260
3! 4! 2! 3*2*1.4*3+2 *1 6*2 12
Permutaciones Circulares
Las permutaciones circulares se utilizan cuando os elementos se van a ordenar en circulo
Por ejemplo
Los comensales en una mesa se van a sentar de modo que el primer elemento que se situe en la mesa determina el principio y el fin de la lista.
La formula para la permutacion circular es PC n-1=n!
Ejercicio
- De cuantas formas distintas pueden sentarse 8 personas alrededor de una mesa redonda.
PC n-1= n!
PC 8-1= 71 =7*6*5*4*3*2*1= 5040
PERMUTACIONES FORMULA REGLAS
1. Entran todos los elementos.
Permutaciones P4= 4! 2. Si importa el orden.
3. No se repiten los elementos.
Con repetición PRn=__Pn__ 222 3333 44 a! b! c! a b c
Circulares PCn-1 = n! Tienen que ser un problema relacionado a un circulo.
Ejercicios de Permutaciones
- ¿Cuantas palabras distintas de cuatro letras se pueden formar? Escriba el listado que se forma.
Pn = 4!
Pn = n! = 4! = 4*3*2*1= 24 palabras
ALEX LAEX ELAX XAEL
AELX LAXE ELXA XALE
AEXL LXAE EXAL XLAE
AXLE LXEA EXLA XLEA
AXEL LEAX EALX XELA
ALXE LAEX EAXL XEAL
2.¿Cuantas palabras diferentes de 5 letras se puede fomar con la palabra LIBRO?
Pn = n! =5! = 5*4*3*2*1= 120 palabras
3.¿Cuantas palabras diferentes de 6 letras se puede formar la palabra TRATAR?
PRn = ____Pn_____
a! b! c!
2,2,2
PR =____P6_____ = 6*5*4*3*2*1 =___360___ = 90 palabras
2! 2! 2! 2*1 * 2*1 * 2*1 4
4.¿Cuantas palabras de 10 letras se puede formar usando la palabra TERMÓMETRO?
PR =____P10____ = 10*9*8*7*6*5*4*3*2*1 = 1814400 = 113400 palabras
2! 2! 2! 2! 2! 2*1 x 2*1 x 2*1 x 2*1 x 2*1 16
Principios Fundamentales del Conteo
La enumeración o conteo puede parecer un proceso obvio que un estudiante aprende al estudio aritmética por primera vez. Pero luego según parece se presta poca atención en lo que se refiere a un desarrollo mas amplio del conteo, conforme el estudiante pasa áreas mas difíciles de las matemáticas como el álgebra, la geometría, la trigonometria y el calculo. En consecuencia deberá servir como advertencia acerca del conteo.
La enumeración no termina con la aritmética, también tiene aplicaciones como: la teoría de códigos, la probabilidad y la estadística.
Reglas de la Suma y Producto
- Si una primera tarea puede realizarse de "m" formas mientras que una segunda tarea puede realizarse de "n" formas, y no es posible realizar ambas tareas de manera simultanea entonces para llevar a cabo cualquiera de ellas.
- Si un procedimiento se puede descomponer en las etapas primera y segunda, si existe "m" resultados posibles de la primera etapa, para cada uno de estos resultados existen "n" resultados posibles para la segunda etapa, entonces el procedimiento total se puede realizar en el orden dado.
CUESTIONARIO
1°-¿Qué son las Técnicas de Conteo?
Las técnicas de conteo son una serie de métodos de probabilidad para contar el número posible de arreglos dentro de un conjunto o varios conjuntos de objetos.
2°-¿Cuando se usan las Técnicas de Conteo?
Estas se usan cuando realizar las cuentas de forma manual se convierte en algo complicado debido a la gran cantidad de objetos y/o variables.
3°-Menciona las Técnicas de Conteo que conozcas.
Diagrama de árbol, permutaciones, combinaciones, variaciones.
4°-¿Que es un Diagrama de Árbol?
Un diagrama de árbol o árbol de probabilidad es una herramienta que se utiliza para determinar si en realidad en el cálculo de muchas opciones se requiere conocer el número de objetos que forman parte del espacio muestral, estos se pueden determinar con la construcción de un diagrama de planta.
5°-¿Que son las Permutaciones?
Se llama permutaciones de "n" elementos a los diferentes grupos que se pueden formar con esos elementos, siguiendo las siguientes reglas.
- Entran todos los elementos.
- Si importa el orden.
- No se repitan los elementos.
6°-¿Que son las Variaciones?
Se llama variaciones ordinarias de m elementos tomados de n en n (m = n) a los distintos grupos formados por n elementos, eligiéndolos de entre los m elementos de que disponemos, de forma que: – No entran todos los elementos.
7°-¿Qué son las combinaciones?
Una combinación es una selección de elementos de una colección, de manera que el orden de selección no importa.
8°-¿Que es una Permutación con Repetición?
Se llama permutaciones con repetición a los grupos de elementos que se forman cuando "n" elementos,donde e primer elemento se repite n veces, el segundo también se repite n veces y así se repiten hasta llegar al final de la lista. Estas agrupaciones deben seguir las siguientes reglas;
- Entran todos los elementos.
- Si importa el orden.
- Si se repiten los elementos.
9°-¿Cuando se utiliza una Permutación Circular?
Las permutaciones circulares se utilizan cuando los elementos se van a ordenar en circulo.
10°-¿Cual es la formula para una Permutacion Circular?
La formula para la permutacion circular es PC n-1=n!
Suscribirse a:
Comentarios (Atom)