Torres Hanoi

1°-¿Que son las Torres de Hanoi?

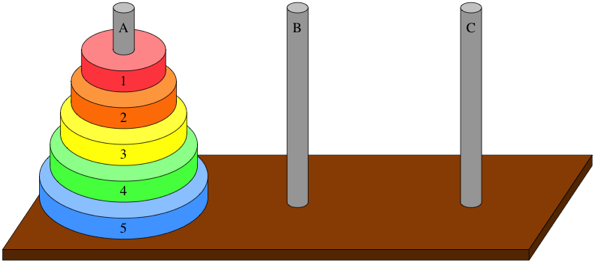
Las Torres de Hanói es un rompecabezas o juego matemático inventado en 1883 por el matemático francés Édouard Lucas. Este juego de mesa individual consiste en un número de discos perforados de radio creciente que se apilan insertándose en uno de los tres postes fijados a un tablero. El objetivo del juego es trasladar la pila a otro de los postes siguiendo ciertas reglas. El problema es muy conocido en la ciencia de la computación y aparece en muchos libros de texto como introducción a la teoría de algoritmos.

La fórmula para encontrar el número de movimientos necesarios para transferir n discos desde un poste a otro es: 2ⁿ - 1

Descripción

El juego, en su forma más tradicional, consiste en tres postes verticales. En uno de los postes se apila un número indeterminado de discos perforados por su centro (elaborados de madera), que determinará la complejidad de la solución. Por regla general se consideran siete discos. Los discos se apilan sobre uno de los postes en tamaño decreciente de abajo a arriba. No hay dos discos iguales, y todos ellos están apilados de mayor a menor radio -desde la base del poste hacia arriba- en uno de los postes, quedando los otros dos postes vacíos. El juego consiste en pasar todos los discos desde el poste ocupado (es decir, el que posee la torre) a uno de los otros postes vacíos. Para realizar este objetivo, es necesario seguir tres simples reglas:

1. Solo se puede mover un disco cada vez y para mover otro los demás tienen que estar en postes.
2. Un disco de mayor tamaño no puede estar sobre uno más pequeño que él mismo.
3. Solo se puede desplazar el disco que se encuentre arriba en cada poste.

Existen diversas formas de llegar a la solución final, todas ellas siguiendo estrategias diversas.

2°-¿Como es el algoritmo para resolver el problema de las Torres de Hanoi?

La solución del problema de las Torres de Hanói es muy fácil de hallar, aunque el número de pasos para resolver el problema crece exponencialmente conforme aumenta el número de discos.Como ya se ha indicado, el número mínimo de movimientos necesarios para resolver un rompecabezas de la Torre de Hanoi es 2ⁿ - 1, donde n es la cantidad de discos.

Una manera sencilla para saber si es posible terminar el "juego" es que si la cantidad de discos es impar la pieza inicial ira a destino y si es par a auxiliar.

Solución simple

Una forma de resolver el problema se fundamenta en el disco más pequeño, el de más arriba en la varilla de origen. En un juego con un número par de discos, el movimiento inicial de la varilla origen es hacia la varilla auxiliar. El disco 2.^o n-1 se debe mover, por regla, a la varilla destino. Luego, el disco n.^o 1 se mueve también a la varilla destino para que quede sobre el disco n.^o 2. A continuación, se mueve el disco que sigue de la varilla origen, en este caso el disco n.^o 3, y se coloca en la varilla auxiliar. Finalmente, el disco n.^o 1 regresa de la varilla destino a la origen (sin pasar por la auxiliar), y así sucesivamente. Es decir, el truco está en el disco más pequeño.

Mediante recursividad

Este problema se suele plantear a menudo en programación, especialmente para explicar la recursividad. Si numeramos los discos desde 1 hasta n, si llamamos origen a la primera pila de discos, destino a la tercera y auxiliar a la intermedia, y si a la función la denomináramos hanoi, con origen, auxiliar y destino como parámetros, el algoritmo de la función sería el siguiente:

El número de movimientos mínimo a realizar para resolver el problema de este modo es de 2ⁿ – 1, siendo n el número de discos.

Iterativa

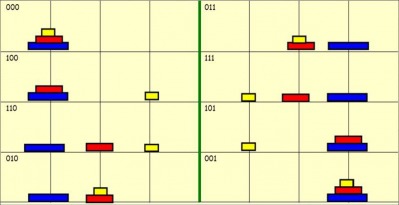
Otra manera de resolver el problema, sin utilizar la recursividad, se basa en el hecho de que para obtener la solución más corta, es necesario mover el disco más pequeño en todos los pasos impares, mientras que en los pasos pares solo existe un movimiento posible que no lo incluye. El problema se reduce a decidir en cada paso impar a cuál de las dos pilas posibles se desplazará el disco pequeño. El algoritmo en cuestión depende del número de discos del problema:

• Si inicialmente se tiene un número impar de discos, el primer movimiento debe ser colocar el disco más pequeño en la pila destino, y en cada paso impar se le mueve a la siguiente pila a su izquierda (o a la pila destino si está en la pila origen).

La secuencia será: destino, auxiliar, origen, destino, auxiliar, origen, etc.

• Si se tiene inicialmente un número par de discos, el primer movimiento debe ser colocar el disco más pequeño en la pila auxiliar, y en cada paso impar se le mueve a la siguiente pila a su derecha (o a la pila origen si está en la pila destino).

La secuencia será: auxiliar, destino, origen, auxiliar, destino, origen, etc.

Una forma equivalente de resolverlo es la siguiente: coloreando los discos pares de un color y los impares de otro, y se resuelve el problema añadiendo la siguiente regla: no colocar juntos dos discos de un mismo color. De esta manera, solo queda un movimiento posible (además del de volver hacia atrás).

Reglas matemáticas de los desplazamientos

A la hora de resolver matemáticamente el problema, se producen numerosas circunstancias matemáticas particulares respecto a la resolución. Son las siguientes:

• La ficha número n (siendo 1 la más pequeña) se mueve por primera vez en el paso número 2^(n-1), y después de ese primer movimiento, se moverá cada 2^n movimientos. De este modo, la ficha 1, se mueve en 1, 3, 5, 7, 9... etc. La ficha 3, se mueve en 4, 12, 20, 28, 36... etc.
• Y el número de veces que se mueve cada ficha es de 2^(n-k),siendo n el número de fichas y k igual a 1 para la ficha más pequeña.
• El número de movimientos mínimo a realizar para resolver el problema es de (2^n)-1, siendo n el número de fichas.
• Todas las fichas impares (siendo 1 la más pequeña) se mueven siguiendo el mismo patrón. Asimismo, todas las fichas pares se mueven siguiendo el patrón inverso a las impares. Por ejemplo: si se quiere mover un número impar de piezas desde la columna 1 hasta la 3, sucederá lo siguiente:

• Todas las fichas impares seguirán este patrón de movimiento: 1 -> 3 -> 2 -> 1 -> 3 -> 2 -> 1 -> 3 -> 2 -> 1.
• Todas las fichas pares seguirán este patrón de movimiento: 1 -> 2 -> 3 -> 1 -> 2 -> 3 -> 1 -> 2 -> 3

Estos patrones dependen únicamente del número de piezas. Si el número de piezas es par, los patrones de las impares serán los de las pares, y viceversa.

• Uniendo la primera regla con la segunda, se sabe siempre qué pieza hay que mover y a qué columna hay que desplazarla, por lo que el problema queda resuelto.

3°¿Es permutacion o combinación?

CUESTIONARIO

1°-¿Qué son las Torres de Hanoi?

La Torres de Hanoi es un rompecabezas o juego matemático.

2°-¿Cuándo se inventaron las Torres de Hanoi?

Fue inventado en 1883 por el matemático francés Édouard Lucas.

3°-¿En que consiste este juego?

Este juego de mesa individual consiste en un número de discos perforados de radio creciente que se apilan insertándose en uno de los tres postes fijados a un tablero. 

4°-¿Cuál es el objetivo del juego?

El objetivo del juego es trasladar la pila a otro de los postes siguiendo ciertas reglas. El problema es muy conocido en la ciencia de la computación y aparece en muchos libros de texto como introducción a la teoría de algoritmos.

5°-¿Cual es la formula para el juego?

La fórmula para encontrar el número de movimientos necesarios para transferir n discos desde un poste a otro es: 2ⁿ - 1

6°-¿Cómo es el algoritmo para resolver el problema de las Torres de Hanoi?

La solución del problema de las Torres de Hanói es muy fácil de hallar, aunque el número de pasos para resolver el problema crece exponencialmente conforme aumenta el número de discos.Como ya se ha indicado, el número mínimo de movimientos necesarios para resolver un rompecabezas de la Torre de Hanoi es 2ⁿ - 1, donde n es la cantidad de discos.

Una manera sencilla para saber si es posible terminar el "juego" es que si la cantidad de discos es impar la pieza inicial ira a destino y si es par a auxiliar.

7°-¿Mediante que procesos se puede resolver el problema de las Torres de Hanoi?

-Solución Simple

-Mediante recursividad

-Iterativa

8°-¿En qué consiste "La solución Simple"?

El disco 2.^o n-1 se debe mover, por regla, a la varilla destino. Luego, el disco n.^o 1 se mueve también a la varilla destino para que quede sobre el disco n.^o 2. A continuación, se mueve el disco que sigue de la varilla origen, en este caso el disco n.^o 3, y se coloca en la varilla auxiliar. Finalmente, el disco n.^o 1 regresa de la varilla destino a la origen (sin pasar por la auxiliar), y así sucesivamente. Es decir, el truco está en el disco más pequeño.

9°-¿En qué consiste la solución "Mediante Recursividad"?

Si numeramos los discos desde 1 hasta n, si llamamos origen a la primera pila de discos, destino a la tercera y auxiliar a la intermedia, y si a la función la denomináramos hanoi, con origen, auxiliar y destino como parámetros, el algoritmo de la función sería el siguiente:

El número de movimientos mínimo a realizar para resolver el problema de este modo es de 2ⁿ – 1, siendo n el número de discos.

10°-¿En qué consiste la solución "Iterativa"?

Se basa en el hecho de que para obtener la solución más corta, es necesario mover el disco más pequeño en todos los pasos impares, mientras que en los pasos pares solo existe un movimiento posible que no lo incluye.

Serie de Fibonacci 

1°-¿Que es la serie de Fibonacci?

En matemáticas la sucesión o serie de Fibonacci es la siguiente sucesión infinita de números naturales:

${\displaystyle 0,1,1,2,3,5,8,13,21,34,55,}$ ${\displaystyle 89,}$ ${\displaystyle 144,}$ ${\displaystyle 233,}$ ${\displaystyle 377,}$ ${\displaystyle 610,}$ ${\displaystyle 987,}$ ${\displaystyle 1597\ldots \,}$

A los elementos de esta sucesión se les llama números de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación, matemática y teoría de juegos. 

También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en las flores de alcachofas y girasoles, en las inflorescencias del brécol romanesco, en la configuración de las piñas de las coníferas, en la reproducción de los conejos y en cómo el ADN codifica el crecimiento de formas orgánicas complejas. De igual manera, se encuentra en la estructura espiral del caparazón de algunos moluscos, como el nautilus. La sucesión comienza con los números 0 y 1,​ y a partir de estos, «cada término es la suma de los dos anteriores», es la relación de recurrencia que la define.

La sucesión de Fibonacci, en ocasiones también conocida como secuencia de Fibonacci o incorrectamente como serie de Fibonacci, es en sí una sucesión matemática infinita. Consta de una serie de números naturales que se suman de a 2, a partir de 0 y 1. Básicamente, la sucesión de Fibonacci se realiza sumando siempre los últimos 2 números (Todos los números presentes en la sucesión se llaman números de Fibonacci) de la siguiente manera:

0,1,1,2,3,5,8,13,21,34...

Fácil, ¿no? (0+1=1 / 1+1=2 / 1+2=3 / 2+3=5 / 3+5=8 / 5+8=13 / 8+13=21 / 13+21=34...) Así sucesivamente, hasta el infinito. Por regla, la sucesión de Fibonacci se escribe así: xn = xn-1 + xn-2.

2°-¿Como es la serie Fibonacci?

Existen diferentes formas para calcular los números de Fibonacci:

1. Partiendo de los números 0 y 1, los números de Fibonacci quedan definidos por la función

2. Función generadora: Una función generadora para una sucesión cualquiera a0, a1, a2,… es la función f(X) = a0 + a1x + a2x2+…, es decir, una serie formal de potencias donde cada coeficiente es un elemento de la sucesión. Los números de Fibonacci tienen la función generadora:

3. Fórmula explícita: Esta manera de calcular los números de Fibonacci utiliza la expresión del número áureo:

CUESTIONARIO

1°-¿Que es la serie de Fibonacci?

En matemáticas la sucesión o serie de Fibonacci es la siguiente sucesión infinita de números naturales:

       

2°-¿Cuando se creo la Serie de Fibonacci?

Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci.

3°-¿En qué ámbitos se aplica dicha serie?

Tiene numerosas aplicaciones en ciencias de la computación, matemática y teoría de juegos. 

4°-¿Cuál es la relación de la sucesión de Fibonacci?

La sucesión comienza con los números 0 y 1,​ y a partir de estos, «cada término es la suma de los dos anteriores», es la relación de recurrencia que la define.

5°-¿Cuál es la regla de la sucesión de Fibonacci?

 Por regla, la sucesión de Fibonacci se escribe así: xn = xn-1 + xn-2.

6°-¿Cuáles son los métodos para calcular los números de Fibonacci?

-Función generadora

-Formula explicita 

-Por la función

7°-¿En que consiste la "Función Generadora"?

Una función generadora para una sucesión cualquiera a0, a1, a2,… es la función f(X) = a0 + a1x + a2x2+…, es decir, una serie formal de potencias donde cada coeficiente es un elemento de la sucesión. Los números de Fibonacci tienen la función generadora:

8°-¿En qué consiste la "Formula Explicita"?

Esta manera de calcular los números de Fibonacci utiliza la expresión del número áureo:

9°-¿Cómo se desarrolla el método"Por la Función"  para calcular los números de Fibonacci ?Partiendo de los números 0 y 1, los números de Fibonacci quedan definidos por la función

10°-¿Cómo es la serie de Fibonacci?

Básicamente, la sucesión de Fibonacci se realiza sumando siempre los últimos 2 números (Todos los números presentes en la sucesión se llaman números de Fibonacci) de la siguiente manera:
                                                       0,1,1,2,3,5,8,13,21,34...

Triángulo de Pascal 

 1°-¿Que es el triangulo de Pascal?

 El triángulo de Pascal es un triángulo de números enteros, infinito y simétrico Se empieza con un 1 en la primera fila, y en las filas siguientes se van colocando números de forma que cada uno de ellos sea la suma de los dos números que tiene encima. Se supone que los lugares fuera del triángulo contienen ceros, de forma que los bordes del triángulo están formados por unos. Aquí sólo se ve una parte; el triángulo continúa por debajo y es infinito. 

 2°-¿Como se construye un Triangulo de Pascal?

El triángulo de Pascal se construye siguiendo un patrón como el que se muestra en la figura de abajo. Se comienza desde la cúspide con el número «1» hacia abajo(infinito), a modo de "árbol"; se clasifica en filas, empezando por la fila cero(el «1» de la cúspide). Este "árbol" tiene nodos, que son cada número que compone el triángulo. Si sumamos dos nodos nos dará de resultado el nodo situado debajo de estos dos, y así sucesivamente. Las diagonales que empiezan desde el «1» situado en la cabeza del triángulo valen siempre 1.

 3°-¿Cuales son las aplicaciones para un triangulo de Pascal? 

 Este triángulo fue ideado para desarrollar las potencias de binomios. Las potencias de binomios vienen dadas por la fórmula: {\displaystyle (a+b)^{n}} {\displaystyle (a+b)^{n}}, dónde a y b son variables cualesquiera y n el exponente que define la potencia. Esta expresión se denomina binomio de Newton. Esta fórmula del binomio de Newton desarrolla los coeficientes de cada fila en el triángulo de Pascal. 

Es por esto que existe una estrecha relación entre el triángulo de Pascal y los binomios de Newton. 

Caras y cruces

El triángulo de Pascal te dice cuántas combinaciones de caras y cruces de pueden salir tirando monedas. Así puedes averiguar la "probabilidad" de cualquier combinación. Por ejemplo, si tiras una moneda tres veces, sólo hay una manera de sacar tres caras (CCC), pero hay tres maneras de sacar dos caras y una cruz (CCX, CXC, XCC), también tres de sacar una cara y dos cruces (CXX, XCX, CXX) y sólo una de sacar tres cruces (XXX). Esta es la pauta "1,3,3,1" en el triángulo de Pascal.

CUESTIONARIO

1°-¿Qué es el Triángulo de Pascal?

El triángulo de Pascal es un triángulo de números enteros, infinito y simétrico 

2°-¿Cómo empieza el Triángulo de Pascal?

Se empieza con un 1 en la primera fila, y en las filas siguientes se van colocando números de forma que cada uno de ellos sea la suma de los dos números que tiene encima.

3°-¿Cómo se construye un Triángulo de Pascal? 

El triángulo de Pascal se construye siguiendo un patrón como el que se muestra en la figura de abajo. Se comienza desde la cúspide con el número «1» hacia abajo(infinito), a modo de "árbol"; se clasifica en filas, empezando por la fila cero(el «1» de la cúspide). 

4°-Explica la función que tienen los Nodos en dicho Triángulo.

Este "árbol" tiene nodos, que son cada número que compone el triángulo. Si sumamos dos nodos nos dará de resultado el nodo situado debajo de estos dos, y así sucesivamente. Las diagonales que empiezan desde el «1» situado en la cabeza del triángulo valen siempre 1.

5°-¿Cuáles son las aplicaciones para un Triángulo de Pascal?

Este triángulo fue ideado para desarrollar las potencias de binomios. Las potencias de binomios vienen dadas por la fórmula: {\displaystyle (a+b)^{n}} {\displaystyle (a+b)^{n}}, dónde a y b son variables cualesquiera y n el exponente que define la potencia. Esta expresión se denomina binomio de Newton. Esta fórmula del binomio de Newton desarrolla los coeficientes de cada fila en el triángulo de Pascal. 

Es por esto que existe una estrecha relación entre el triángulo de Pascal y los binomios de Newton. 

6°-Explica las Caras y Cruces en el Triángulo de Pascal.

El triángulo de Pascal te dice cuántas combinaciones de caras y cruces de pueden salir tirando monedas. Así puedes averiguar la "probabilidad" de cualquier combinación. Por ejemplo, si tiras una moneda tres veces, sólo hay una manera de sacar tres caras (CCC), pero hay tres maneras de sacar dos caras y una cruz (CCX, CXC, XCC), también tres de sacar una cara y dos cruces (CXX, XCX, CXX) y sólo una de sacar tres cruces (XXX). Esta es la pauta "1,3,3,1" en el triángulo de Pascal.

7°-¿Porque se llama Triangulo de Pascal?

Es llamado así en honor al filósofo y matemático francés Blaise Pascal, quien introdujo esta notación en 1654, en su Traité du triangle arithmétique.

8°-¿Cómo se puede generalizar el Triángulo de Pascal?

El triángulo de Pascal se puede generalizar a dimensiones mayores. La versión de tres dimensiones se llama pirámide de Pascal o tetraedro de Pascal, mientras que las versiones más generales son llamadas simplex de Pascal.

9°-¿Cuándo fue la primera representación del Triangulo de Pascal?

La primera representación explícita de un triángulo de coeficientes binomiales data del siglo X, en los comentarios de los Chandas Shastra, un libro antiguo indio de prosodia del sánscrito escrito por Pingala alrededor del año 200 a.C

10°-¿Cuál es el uso de este Triángulo?

Este triángulo fue ideado para desarrollar las potencias de binomios. 

Ejercicios De Diagrama de Árbol

https://es.scribd.com/document/401409195/Diagrama-de-Arbol

CUESTIONARIO

1°-¿Qué es un Diagrama de Árbol?

Un diagrama de árbol o árbol de probabilidad es una herramienta que se utiliza para determinar si en realidad en el cálculo de muchas opciones se requiere conocer el número de objetos que forman parte del espacio muestral, estos se pueden determinar con la construcción de un diagrama de planta.

2°-¿Para que se usa un Diagrama de Árbol?

Los diagramas en árbol son especialmente útiles para resolver problemas con experimentos compuestos, es decir, aquellos donde realizamos más de un experimento aleatorio.

3°-Menciona experimentos donde se pueda usar el diagrama de Árbol.

Algunos ejemplos de experimentos compuestos son: tirar dos monedas al aire, y mirar si salen dos caras, contar si hay dos mujeres de entre tres hijos, sacar dos bolas de una urna, y mirar si hay una roja y una azul.

4°-¿Cómo se construye un Diagrama de Árbol?

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad. Cada una de estas ramas se conoce como rama de primera generación.

5°-¿Cuál es el principio que se usa en un Diagrama de Árbol?

Existe un principio sencillo de los diagramas de árbol que hace que éstos sean mucho más útiles para los cálculos rápidos de probabilidad: multiplicamos las probabilidades si se trata de ramas adyacentes (contiguas)

6°-Menciona las características de un Diagrama de Árbol.

• Un diagrama de árbol parte de lo general y va hacia lo específico, es decir, la base es el problema y las ramificaciones son los niveles subsecuentes o causas.
• Un diagrama de árbol es útil en la construcción de agrupación, bien sean combinaciones, variaciones o permutaciones.

7°-¿Cómo crear un Diagrama de Árbol experimental?

En la construcción de un diagrama en árbol se comienza colocando una rama para cada una de las posibilidades y se acompaña de su respectiva probabilidad, estas ramas son conocidas como ramas de primera generación.

Al final de cada ramificación de primera generación, a la vez se constituye un nudo, del cual salen nuevas ramas, estas se conocen a modo de ramas de segunda generación

8°-¿Cómo se caracteriza un Diagrama de Árbol de decisión?
Un diagrama de árbol de decisión se caracteriza por no tener demasiados elementos, los elementos clave se llaman nodos y se representan con un círculo o un cuadrado, las ramas son líneas que conectan los nodos y otras ramas hasta alcanzar el resultado deseado.

9°-¿Que utilidad tiene esta herramienta para las empresas?
Las empresas utilizan este método en diferentes procesos y procedimientos, en virtud de que permiten identificar las acciones, tareas y decisiones que son necesarias para desarrollar soluciones y mejoras en el rendimiento y eficiencia de la misma.

10°-¿Qué utilidad tiene esta herramienta en la vida cotidiana?
En la vida misma se pueden aplicar los diagramas de árbol, como una herramienta a la hora de elegir, combinar o desechar algunas opciones que se nos presentan ante sucesos, eventualidades o problemas.