Serie de Fibonacci 

1°-¿Que es la serie de Fibonacci?

En matemáticas la sucesión o serie de Fibonacci es la siguiente sucesión infinita de números naturales:

${\displaystyle 0,1,1,2,3,5,8,13,21,34,55,}$ ${\displaystyle 89,}$ ${\displaystyle 144,}$ ${\displaystyle 233,}$ ${\displaystyle 377,}$ ${\displaystyle 610,}$ ${\displaystyle 987,}$ ${\displaystyle 1597\ldots \,}$

A los elementos de esta sucesión se les llama números de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación, matemática y teoría de juegos. 

También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en las flores de alcachofas y girasoles, en las inflorescencias del brécol romanesco, en la configuración de las piñas de las coníferas, en la reproducción de los conejos y en cómo el ADN codifica el crecimiento de formas orgánicas complejas. De igual manera, se encuentra en la estructura espiral del caparazón de algunos moluscos, como el nautilus. La sucesión comienza con los números 0 y 1,​ y a partir de estos, «cada término es la suma de los dos anteriores», es la relación de recurrencia que la define.

La sucesión de Fibonacci, en ocasiones también conocida como secuencia de Fibonacci o incorrectamente como serie de Fibonacci, es en sí una sucesión matemática infinita. Consta de una serie de números naturales que se suman de a 2, a partir de 0 y 1. Básicamente, la sucesión de Fibonacci se realiza sumando siempre los últimos 2 números (Todos los números presentes en la sucesión se llaman números de Fibonacci) de la siguiente manera:

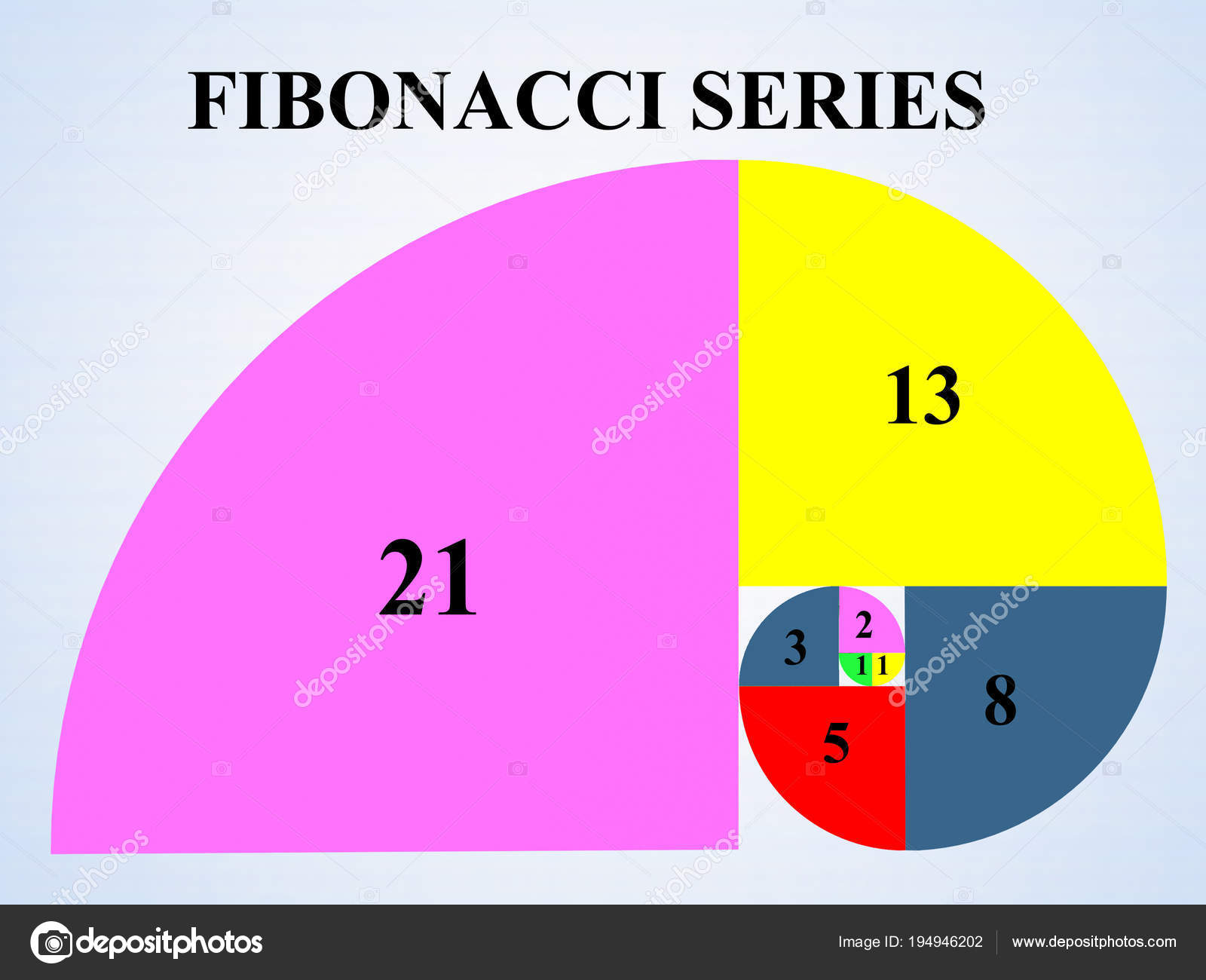
0,1,1,2,3,5,8,13,21,34...

Fácil, ¿no? (0+1=1 / 1+1=2 / 1+2=3 / 2+3=5 / 3+5=8 / 5+8=13 / 8+13=21 / 13+21=34...) Así sucesivamente, hasta el infinito. Por regla, la sucesión de Fibonacci se escribe así: xn = xn-1 + xn-2.

2°-¿Como es la serie Fibonacci?

Existen diferentes formas para calcular los números de Fibonacci:

1. Partiendo de los números 0 y 1, los números de Fibonacci quedan definidos por la función

2. Función generadora: Una función generadora para una sucesión cualquiera a0, a1, a2,… es la función f(X) = a0 + a1x + a2x2+…, es decir, una serie formal de potencias donde cada coeficiente es un elemento de la sucesión. Los números de Fibonacci tienen la función generadora:

3. Fórmula explícita: Esta manera de calcular los números de Fibonacci utiliza la expresión del número áureo:

CUESTIONARIO

1°-¿Que es la serie de Fibonacci?

En matemáticas la sucesión o serie de Fibonacci es la siguiente sucesión infinita de números naturales:

       

2°-¿Cuando se creo la Serie de Fibonacci?

Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci.

3°-¿En qué ámbitos se aplica dicha serie?

Tiene numerosas aplicaciones en ciencias de la computación, matemática y teoría de juegos. 

4°-¿Cuál es la relación de la sucesión de Fibonacci?

La sucesión comienza con los números 0 y 1,​ y a partir de estos, «cada término es la suma de los dos anteriores», es la relación de recurrencia que la define.

5°-¿Cuál es la regla de la sucesión de Fibonacci?

 Por regla, la sucesión de Fibonacci se escribe así: xn = xn-1 + xn-2.

6°-¿Cuáles son los métodos para calcular los números de Fibonacci?

-Función generadora

-Formula explicita 

-Por la función

7°-¿En que consiste la "Función Generadora"?

Una función generadora para una sucesión cualquiera a0, a1, a2,… es la función f(X) = a0 + a1x + a2x2+…, es decir, una serie formal de potencias donde cada coeficiente es un elemento de la sucesión. Los números de Fibonacci tienen la función generadora:

8°-¿En qué consiste la "Formula Explicita"?

Esta manera de calcular los números de Fibonacci utiliza la expresión del número áureo:

9°-¿Cómo se desarrolla el método"Por la Función"  para calcular los números de Fibonacci ?Partiendo de los números 0 y 1, los números de Fibonacci quedan definidos por la función

10°-¿Cómo es la serie de Fibonacci?

Básicamente, la sucesión de Fibonacci se realiza sumando siempre los últimos 2 números (Todos los números presentes en la sucesión se llaman números de Fibonacci) de la siguiente manera:
                                                       0,1,1,2,3,5,8,13,21,34...